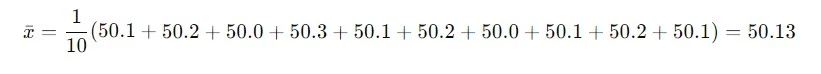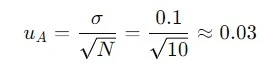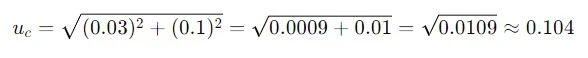Rumus Ketidakpastian Pengukuran: Pemahaman dan Penerapannya di Laboratorium

Pengukuran yang akurat sangat penting dalam laboratorium untuk memastikan hasil yang dapat diandalkan dan diterima. Ketidakpastian pengukuran adalah parameter yang mencerminkan sejauh mana hasil pengukuran mendekati nilai sebenarnya.

Memahami dan menghitung ketidakpastian pengukuran membantu laboratorium dalam meningkatkan akurasi dan keandalan hasilnya.

Daftar Isi

Konsep Dasar Ketidakpastian Pengukuran

Rumus Ketidakpastian Pengukuran

1. Konsep Dasar Ketidakpastian Pengukuran

1.1. Pengertian Ketidakpastian Pengukuran

Ketidakpastian pengukuran adalah parameter yang menunjukkan sejauh mana hasil pengukuran mendekati nilai sebenarnya dari besaran yang diukur. Ketidakpastian pengukuran tidak dapat dihilangkan sepenuhnya, tetapi dapat diminimalkan melalui berbagai teknik dan metode.

1.2. Jenis-Jenis Ketidakpastian

Ketidakpastian Tipe A (Evaluasi Statistik)

Ketidakpastian tipe A dihitung berdasarkan analisis statistik dari serangkaian pengukuran berulang. Penggunaan statistik deskriptif seperti rata-rata, simpangan baku, dan distribusi data sangat penting dalam evaluasi ini.

Ketidakpastian Tipe B (Evaluasi Non-Statistik)

Ketidakpastian tipe B diperoleh dari sumber lain selain data pengukuran langsung, seperti sertifikat kalibrasi, spesifikasi alat, atau literatur ilmiah. Evaluasi tipe B sering kali melibatkan estimasi yang tidak didasarkan pada analisis statistik.

1.3. Langkah-Langkah Menghitung Ketidakpastian Pengukuran

1.3.1. Identifikasi Sumber Ketidakpastian

Langkah pertama dalam menghitung ketidakpastian adalah mengidentifikasi semua sumber ketidakpastian yang mungkin mempengaruhi hasil pengukuran. Sumber ketidakpastian dapat berasal dari:

Alat pengukur
Metode pengukuran
Lingkungan pengukuran
Operator atau pengamat

1.3.2. Estimasi Ketidakpastian Pengukuran

Setelah mengidentifikasi sumber ketidakpastian, langkah berikutnya adalah membuat estimasi awal terhadap masing-masing sumber ketidakpastian. Estimasi ini melibatkan penentuan kontribusi ketidakpastian dari setiap sumber.

2.3.3. Pengumpulan Data dan Analisis Statistik

Untuk ketidakpastian tipe A, data pengukuran dikumpulkan dan dianalisis secara statistik. Beberapa langkah dalam analisis statistik meliputi:

Menghitung rata-rata (̅x)
Menghitung simpangan baku (σ)

Rumus rata-rata (̅x) adalah:

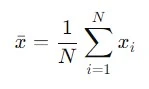
di mana N adalah jumlah pengukuran, dan x_i adalah nilai pengukuran ke-i.

Rumus simpangan baku (σ) adalah:

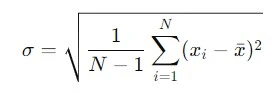
1.3.4. Perhitungan Ketidakpastian Tipe A

Setelah menghitung simpangan baku, ketidakpastian tipe A (u_A) dapat dihitung sebagai:

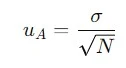
1.3.5. Perhitungan Ketidakpastian Tipe B

Ketidakpastian tipe B (u_B) dihitung berdasarkan data dari sumber non-statistik. Misalnya, jika alat pengukur memiliki ketidakpastian kalibrasi sebesar 0.1 mm, maka u_B adalah 0.1 mm.

1.3.6. Penggabungan Ketidakpastian Tipe A dan Tipe B

Ketidakpastian total (u_c) adalah gabungan dari ketidakpastian tipe A dan tipe B, yang dihitung dengan rumus:

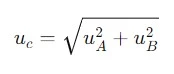
1.3.7. Menghitung Ketidakpastian Diperluas

Ketidakpastian diperluas (U) dihitung dengan mengalikan ketidakpastian gabungan (u_c) dengan faktor cakupan (k), yang biasanya bernilai 2 untuk tingkat kepercayaan sekitar 95%.

1.4. Contoh Perhitungan Ketidakpastian Pengukuran

Contoh Kasus:

Misalkan kita mengukur panjang suatu benda dengan penggaris yang memiliki ketidakpastian kalibrasi sebesar 0.1 mm (tipe B). Kita melakukan 10 pengukuran dan mendapatkan hasil sebagai berikut (dalam mm): 50.1, 50.2, 50.0, 50.3, 50.1, 50.2, 50.0, 50.1, 50.2, 50.1.

Menghitung rata-rata (̅x):
Menghitung simpangan baku (σ):
Menghitung ketidakpastian tipe A (u_A):
Menggabungkan ketidakpastian tipe A dan tipe B untuk mendapatkan ketidakpastian total (u_c):
Menghitung ketidakpastian diperluas (U) dengan faktor cakupan k=2:

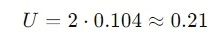
Jadi, panjang benda yang diukur adalah 50.13 mm dengan ketidakpastian diperluas sebesar ±0.21 mm. Hasil ini dapat dilaporkan sebagai “50.13 ± 0.21 mm”.

Dengan memahami dan menerapkan langkah-langkah ini, laboratorium dapat menghitung ketidakpastian pengukuran secara lebih akurat, sehingga meningkatkan keandalan dan kredibilitas hasil pengukurannya.

Contoh Penerapan:

Misalkan kita mengukur panjang suatu benda dengan penggaris yang memiliki ketidakpastian kalibrasi sebesar 0.1 mm (tipe B). Kita melakukan 10 pengukuran dan mendapatkan simpangan baku 0.05 mm (tipe A). Maka, ketidakpastian gabungan adalah:

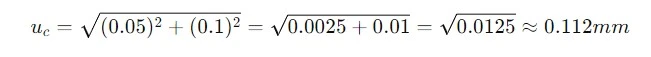
Dengan faktor cakupan :

1.5 Penggunaan Ketidakpastian Pengukuran dalam Laporan Hasil

Ketidakpastian pengukuran harus dilaporkan bersama hasil pengukuran untuk memberikan gambaran lengkap tentang akurasi. Misalnya, jika panjang yang diukur adalah 50 mm, hasilnya dilaporkan sebagai:

1.6 Tips dan Praktik Terbaik untuk Mengurangi Ketidakpastian Pengukuran

Kalibrasi Peralatan: Lakukan kalibrasi secara berkala untuk memastikan alat pengukur berfungsi dengan baik.
Pelatihan Personel: Pastikan personel laboratorium terlatih dan kompeten dalam melakukan pengukuran.
Pemeliharaan Kondisi Lingkungan: Jaga kondisi lingkungan laboratorium agar tetap stabil, seperti suhu dan kelembaban.
Prosedur Operasi Standar (SOP): Gunakan SOP yang ketat untuk mengurangi variasi dalam proses pengukuran.

Kesimpulan

Memahami dan menghitung ketidakpastian pengukuran adalah langkah penting dalam memastikan hasil laboratorium yang akurat dan andal. Dengan menerapkan teknik yang tepat dan menjaga kondisi laboratorium yang stabil, ketidakpastian pengukuran dapat diminimalkan, sehingga meningkatkan kepercayaan terhadap hasil pengukuran.

Apakah Anda ingin memahami lebih dalam tentang konsep dan metode perhitungan ketidakpastian pengukuran? Ingin meningkatkan akurasi dan keandalan hasil pengukuran di laboratorium Anda? Bergabunglah dengan kami di SPIN Training & Consulting!

Hubungi kami sekarang untuk informasi lebih lanjut dan jadwal pelatihan yang tersedia di di halaman ini atau kontak via WhatsApp di nomor 0813-2145-5501 untuk meminta penawaran training yang Anda perlukan.